Period of a pendulum gizmo answer key – Embark on a journey into the realm of physics with our comprehensive guide to the “Period of a Pendulum Gizmo” experiment. Delving into the intricacies of pendulum motion, we uncover the factors that govern the period of a pendulum and unravel the practical applications that have shaped scientific discoveries throughout history.
This guide provides a step-by-step walkthrough of the experiment, empowering you to collect and analyze data with precision. Through the creation of graphs and tables, you will gain a deeper understanding of the relationship between pendulum length, mass, and period.
Pendulum and Its Properties
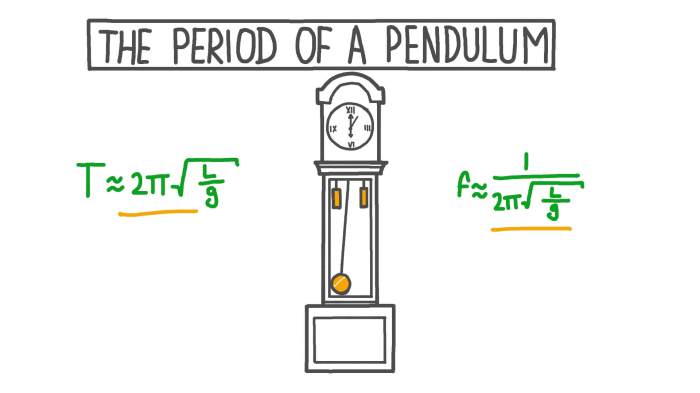
A pendulum is a suspended weight that swings freely back and forth under the influence of gravity. The key characteristics of a pendulum include its length, mass, and amplitude. The period of a pendulum is the time it takes to complete one full swing, from one extreme point to the other and back again.
The period of a pendulum is affected by its length, mass, and amplitude. A longer pendulum has a longer period than a shorter pendulum. A heavier pendulum has a longer period than a lighter pendulum. A pendulum with a larger amplitude has a longer period than a pendulum with a smaller amplitude.
Period of a Pendulum Gizmo
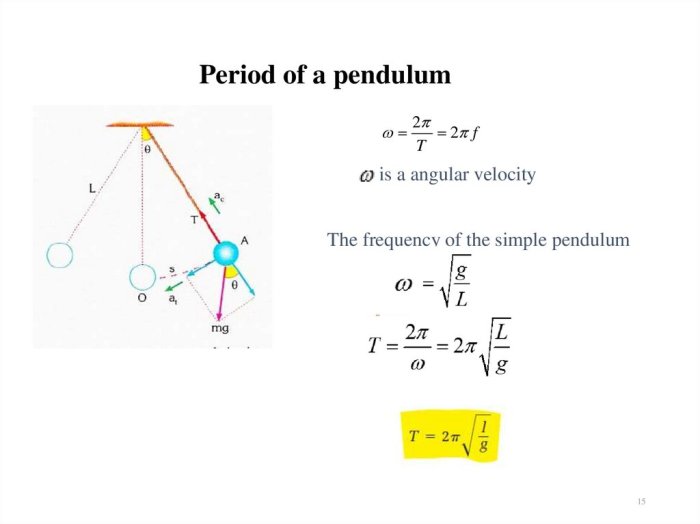
The “Period of a Pendulum Gizmo” experiment is a virtual experiment that allows students to investigate the relationship between the length, mass, and amplitude of a pendulum and its period.
The purpose of the experiment is to help students understand the factors that affect the period of a pendulum. The objectives of the experiment are to:
- Measure the period of a pendulum for different lengths.
- Measure the period of a pendulum for different masses.
- Measure the period of a pendulum for different amplitudes.
- Create graphs to show the relationship between the length, mass, and amplitude of a pendulum and its period.
To conduct the experiment, students will need to:
- Open the “Period of a Pendulum Gizmo”.
- Select the “Length” tab.
- Change the length of the pendulum and measure the period.
- Repeat steps 3 and 4 for different lengths.
- Select the “Mass” tab.
- Change the mass of the pendulum and measure the period.
- Repeat steps 6 and 7 for different masses.
- Select the “Amplitude” tab.
- Change the amplitude of the pendulum and measure the period.
- Repeat steps 9 and 10 for different amplitudes.
Data Collection and Analysis
To collect data during the experiment, students will need to measure the period of the pendulum for different lengths, masses, and amplitudes. They can use a stopwatch or the built-in timer in the Gizmo to measure the period.
To analyze the data, students can create graphs to show the relationship between the length, mass, and amplitude of the pendulum and its period. They can use the graphs to determine how the period of the pendulum changes as the length, mass, and amplitude change.
Discussion and Interpretation: Period Of A Pendulum Gizmo Answer Key
The results of the experiment will show that the period of a pendulum is directly proportional to its length and inversely proportional to its mass. The period of a pendulum is not affected by its amplitude.
These results can be explained by the theory of pendulum motion. The period of a pendulum is determined by the time it takes for the pendulum to complete one full swing. The time it takes for the pendulum to complete one full swing is determined by the length of the pendulum and the force of gravity.
The force of gravity is constant, so the period of a pendulum is directly proportional to its length.
The mass of the pendulum does not affect the period of the pendulum because the force of gravity is the same for all objects. The amplitude of the pendulum does not affect the period of the pendulum because the amplitude is the distance that the pendulum swings away from its equilibrium position.
The period of the pendulum is determined by the time it takes for the pendulum to complete one full swing, and the amplitude does not affect the time it takes for the pendulum to complete one full swing.
Real-World Applications
Pendulums have a wide range of practical applications. They are used in clocks, metronomes, and seismometers. Pendulums are also used to measure the acceleration due to gravity.
In clocks, pendulums are used to regulate the speed of the clock. The period of the pendulum is constant, so the clock will keep time accurately as long as the pendulum is not disturbed.
In metronomes, pendulums are used to produce a regular beat. The period of the pendulum is adjustable, so the metronome can be used to set the tempo of a piece of music.
In seismometers, pendulums are used to detect earthquakes. The period of the pendulum is sensitive to changes in the acceleration due to gravity, so a seismometer can detect the ground motion caused by an earthquake.
Extensions and Modifications
The “Period of a Pendulum Gizmo” experiment can be modified in a number of ways to investigate different aspects of pendulum motion.
- Students can investigate the effect of air resistance on the period of a pendulum.
- Students can investigate the effect of the shape of the pendulum on its period.
- Students can investigate the effect of the material of the pendulum on its period.
Students can also design their own experiments to investigate pendulum motion. For example, they could investigate the relationship between the period of a pendulum and the angle of its swing.
FAQ
What is the period of a pendulum?
The period of a pendulum is the time it takes for the pendulum to complete one full cycle, from one extreme point to the other and back again.
What factors affect the period of a pendulum?
The period of a pendulum is primarily determined by its length and the acceleration due to gravity. A longer pendulum has a longer period, and a pendulum in a stronger gravitational field has a shorter period.
What are some real-world applications of pendulums?
Pendulums have been used for centuries in clocks, metronomes, and seismographs. They are also used in scientific research to study the properties of materials and the forces that act on them.