Aas and isosceles triangles common core geometry homework – Delving into the realm of geometry, this comprehensive exploration of AAS and isosceles triangles unveils their intriguing properties and applications. Rooted in the Common Core geometry standards, this guide empowers students with a deep understanding of these fundamental concepts, equipping them to tackle real-world challenges.
Unraveling the intricate relationships between angles and side lengths, we delve into the unique characteristics of AAS triangles. Moreover, the inherent properties of isosceles triangles become invaluable tools for solving complex geometry problems. Through step-by-step problem-solving strategies and engaging practice exercises, students gain a mastery of these concepts.
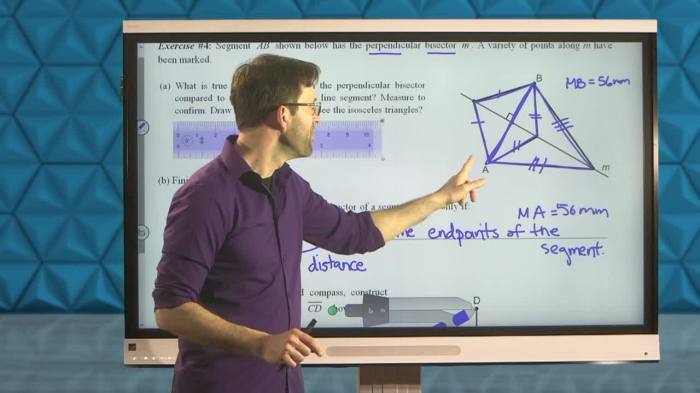
AAS and Isosceles Triangles
In geometry, AAS and isosceles triangles are two important types of triangles with distinct properties and applications.
Key Concepts
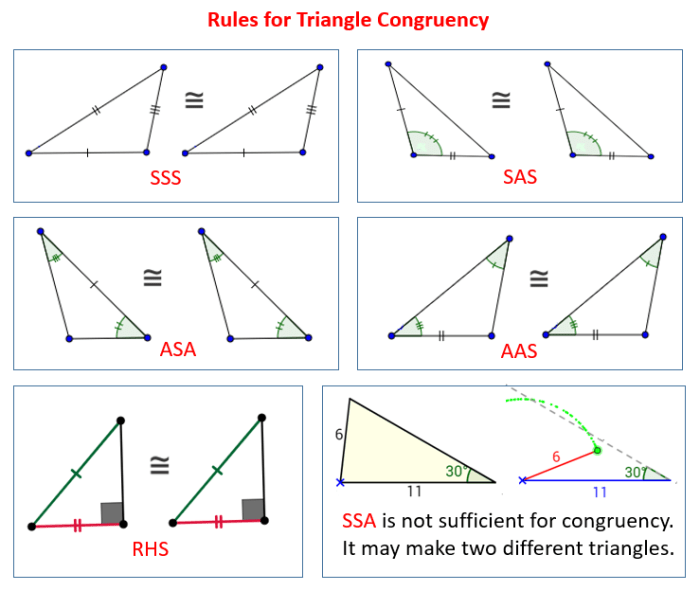
AAS triangles (Angle-Angle-Side triangles) are triangles in which two angles and a non-included side are known. -*Isosceles triangles are triangles with two equal sides.
Properties of AAS triangles:
- If two angles and a non-included side of a triangle are known, the triangle is uniquely determined.
- The angles opposite the equal sides are equal.
- The base angles (angles opposite the equal sides) are congruent.
Properties of isosceles triangles:
- The base angles are congruent.
- The angles opposite the equal sides are equal.
- The altitude drawn from the vertex to the base bisects the base and the angle at the vertex.
Common Core Standards
The Common Core State Standards for Geometry include several standards related to AAS and isosceles triangles:
- G-CO.12: Prove and apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
- G-CO.13: Prove and apply the Angle Bisector Theorem to determine the measure of an angle formed by an angle bisector in a triangle.
- G-CO.14: Prove and apply the Triangle Inequality Theorem to determine whether a triangle exists given the side lengths.
Geometric Relationships
In AAS triangles, the unknown angle can be found using the fact that the sum of the angles in a triangle is 180 degrees.
In isosceles triangles, the unknown side length can be found using the Pythagorean Theorem or the fact that the altitude drawn from the vertex to the base bisects the base.
Problem Solving
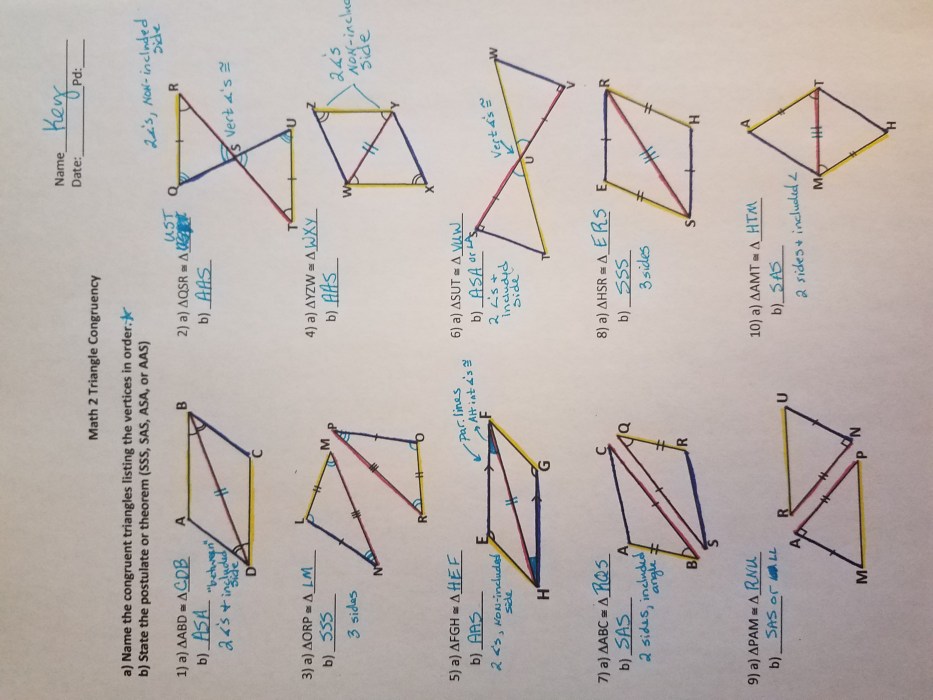
To solve AAS triangle problems, use the following steps:
- Label the known angles and side.
- Use the fact that the sum of the angles in a triangle is 180 degrees to find the unknown angle.
- Use the properties of AAS triangles to find the remaining side lengths.
To solve isosceles triangle problems, use the following steps:
- Label the known side and angles.
- Use the properties of isosceles triangles to find the unknown angles.
- Use the Pythagorean Theorem or the fact that the altitude drawn from the vertex to the base bisects the base to find the remaining side lengths.
Applications, Aas and isosceles triangles common core geometry homework
AAS and isosceles triangles have numerous real-world applications, including:
- Architecture: Designing roofs, bridges, and other structures.
- Engineering: Designing bridges, airplanes, and other machines.
- Surveying: Measuring distances and angles in land surveying.
- Navigation: Determining the location of a ship or aircraft.
Helpful Answers: Aas And Isosceles Triangles Common Core Geometry Homework
What is an AAS triangle?
An AAS triangle is a triangle in which two angles and one non-included side are known.
What is an isosceles triangle?
An isosceles triangle is a triangle in which two sides are equal in length.
How can I solve AAS triangle problems?
To solve AAS triangle problems, you can use the Law of Sines or the Law of Cosines.
How can I solve isosceles triangle problems?
To solve isosceles triangle problems, you can use the Pythagorean Theorem or the properties of isosceles triangles.